円は何角形なのか

2020.01.27

円は何角形なのか

今日は小ネタです。

三角形、四角形、五角形、六角形と辺と頂点を増やしていくと段々と円に近づいていくことがお分かりになると思います。

下図のようにウェブ上ではどんなに綺麗な円に見えても、拡大していくと、ぼやけた多角形であることが分かります。

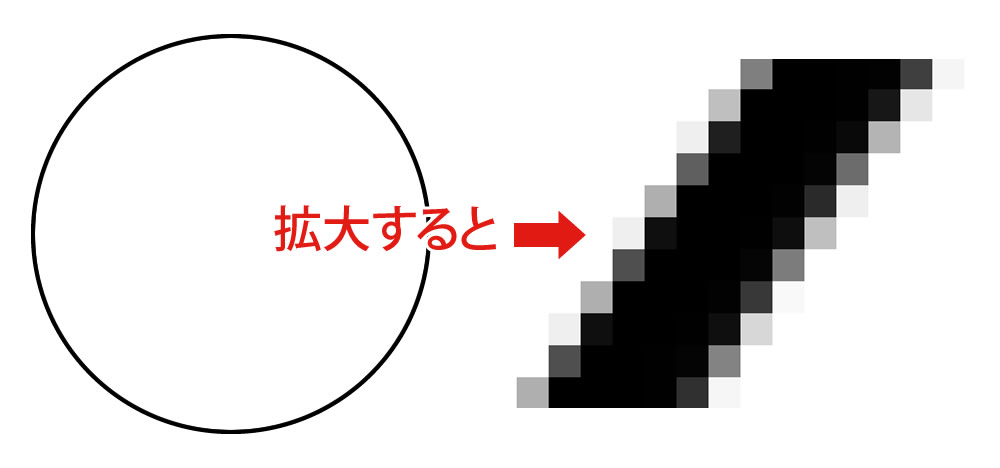
では、何角形から円に見えるのか、円と読んで差し支えないものになるのか。
興味を持った方も多いのではないでしょうか。

答えは六万五千五百三十七角形だそうです。
正65537角形は65537本の辺と65537個の頂点を持ち、定規とコンパスによる作図が可能だそうです。

カール・フリードリヒ・ガウスが1801年に定規とコンパスで作図可能であることを証明し、ヨハン・グスタフ・ヘルメスは、10年の歳月をかけて正65537角形の作図法を調べ、1894年に200ページに及ぶ計算の要旨のみの報告を雑誌に発表したそうです。

今ではコンピューターによって簡単に作図できますが、定規とコンパスによる作図は膨大な作業量になるそうです。

正65537角形よりもさらに踏み込んだ、無限角形は円と呼べるのか否かの議論は哲学的な領域に達するそうです。

まぁ、真円は理論上しか存在しないので考えても仕方ないのですが、考えても仕方ないことの追求は間接的に物事を先に進めることになるので少し考えてみても面白いかも知れませんよ。